Assume we have two sets A and B. We have the following set operations in python,
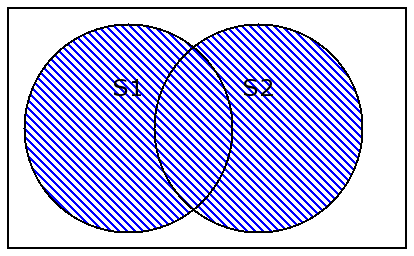
A | Breturns the union.
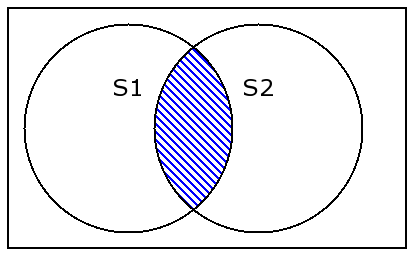
A & Breturns the intersection.
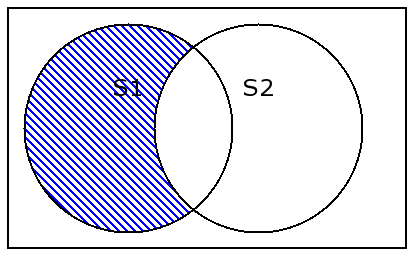
A - Breturns the difference.
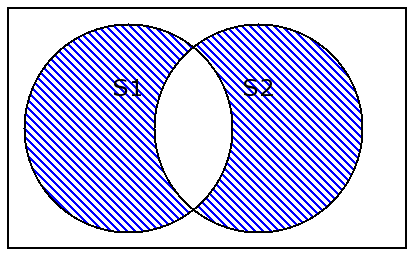
A ^ Breturns the symmetric difference.
Let's talk about the bitwise operators in python,
<<, >>, &, |, ~, ^.
They usually operate on numbers but instead of treating them like a single value, they treat them as a string of bits written in 2's complement binary. 2's complement is calculated by inverting the bits and adding 1.
$ (2)_{10} = 010 \\ (5)_{10} = 0101 \\ (9)_{10} = 01001 \\ (20)_{10} = 010100 $
A negative integers -x is written in binary as x-1 and all the bits complemented. For example, -4 is complement(4-1) = complement(3) = ...1111111100.
The binary form of negative numbers in written with leading 1s instead on 0s. Python uses infinite number of bits. For example, -5 is treated by the bitwise operators in python as ...111111111011. -4 is treated by the bitwise operators in python as ...11111111100.
x << y
Returns the bits of x shifted to the left by y places (the new bits on the left are 0). The same as x * (2**y).
$(11)_{10}$ << $(3)_{10}$ = 1011 << $(3)_{10}$ = 1011000
x = 11
y = 3
a = x << y
a
88
x*(2**y)
88
bin(x)
'0b1011'
bin(a)
'0b1011000'
bin(x*(2**y))
'0b1011000'
x >> y
Returns the bits of x shifted to the right by y places. The same as x // (2**y).
$(11)_{10}$ >> $(3)_{10}$ = 1011 >> $(3)_{10}$ = 1
a = x >> y
a
1
x // (2**y)
1
bin(a)
'0b1'
bin(x//(2**y))
'0b1'
x & y
Performs a bitwise AND operation. Each bit in the output is 1 if the corresponding bits in x and y are 1, otherwise it's 0.
$(11)_{10}$ & $(7)_{10}$ = 1011 & 111 = 11 = $(3)_{10}$
x = 11
y = 7
a = x & y
a
3
bin(a)
'0b11'
x | y
Performs a bitwise OR operation. Each bit in the output is 1 if the corresponding bits in x or y are 1, otherwise it's 0.
$(11)_{10}$ & $(7)_{10}$ = 1011 & 111 = 1111 = $(15)_{10}$
a = x | y
a
15
bin(a)
'0b1111'
~x
Returns the complement of x.
~$(11)_{10}$ = ~1011 = 10100 = $-(12)_{10}$
a = ~x
a
-12
x ^ y
Performs a bitwise exclusive OR. Each bit in the output is the same as the corresponding bit in x if that bit in y is 0. The output bit is the complement of the corresponding bit in x if that bit in y is 1.
$(11)_{10}$ ^ $(7)_{10}$ = 1011 & 111 = 1100 = $(12)_{10}$
a = x ^ y
a
12
Assume we have two sets A and B. We have the following set operations in python,
A | B returns the union.
A & B returns the intersection.
A - B returns the difference.
A ^ B returns the symmetric difference.